这是读书时候的一个小作业，仅贡参考~

Dec,2018 Cosmology Homework

宇宙回溯时间与红移关系：

t0−t=1H0∫0zdz′(1+z′)(1+z′)2(1+Ωm∗z′)−z′(z′+2)ΩΛt_{0}-t=\frac{1}{H_{0}}\int^z_0\frac{dz'}{(1+z')\sqrt{(1+z')^2(1+\Omega_m*z')-z'(z'+2)\Omega_{\Lambda}}}

宇宙学参数：

H0=71  km  s−1  Mpc−1H_{0}=71\;km\;s^{-1}\;Mpc^{-1}

Ωm=0.3ΩΛ=0.7\Omega_m=0.3 \quad\Omega_{\Lambda}=0.7

语言：Fortran95（运算），python3（画图）

代码：

​ 运算部分：

program main
implicit none
integer*4,parameter :: num=100
integer*4 :: i
real*8 :: h
real*8,dimension(num) :: time,logz
real*8,parameter :: h0=1/(3.09d17)
external t

h=0.71
open(66,file='logz.txt')
open(77,file='time.txt')
write(66,*)'logz'
write(77,*)'time'
do i=1,num
	logz(i)=0.+3.5/num*i
	call qromb(t,0.0d0,10**logz(i),time(i))
	time(i)=1./(h*h0)*time(i)     !in unit of s
	write(66,'(f7.3)')logz(i)
	write(77,'(e16.7)')time(i)
enddo
end program main

function t(zpr)
implicit none
real*8 ::zpr,omegal,omegam,t
omegal=0.7;omegam=0.3
t=1./((1+zpr)*sqrt((1+zpr)**2*(1+omegam*zpr)-zpr*(zpr+2)*omegal))
end function t

include 'mathlib/trapzd.f90'
include 'mathlib/qromb.f90'
include 'mathlib/polint.f90'

​ 画图部分：

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import matplotlib

zlog=pd.read_csv('logz.txt')
time=pd.read_csv('time.txt')
time=time/(365*24*3600*10**8)   #change unit from s to Billion years

matplotlib.rcParams['xtick.direction'] = 'in'
matplotlib.rcParams['ytick.direction'] = 'in'
plt.figure(figsize=(8,8))
plt.plot(zlog,time,linewidth=1.2,c='r')
plt.xlabel(r'$Redshift\;in\;unit\;of\;[\log\;z]$')
plt.ylabel(r'$Time\;in\;unit\;of\;[10^8\;years]$')
plt.title(r'$Cosmos\;retrospective\;time\;versus\;redshift$')
plt.xlim(0.03)
plt.ylim(80)
plt.savefig('picresult.jpg')

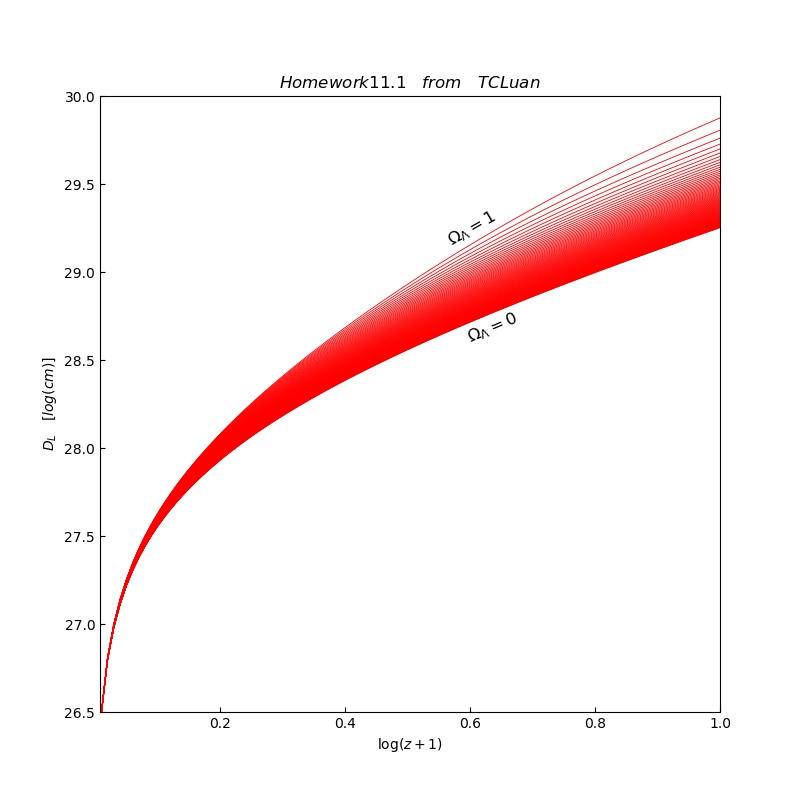
结果图：