如何理解在射电观测中温度的概念？

你是否曾感到好奇，明明我们使用射电望远镜观测的是信号是强度(Intensity)，但是为什么射电领域大家都常常使用“温度”🌡️来描述呢？阅读此文，或许能帮你有一个清晰的理解👏

特别鸣谢：感谢🏫Nakashima Junichi教授耐心地教导以及详细丰富的总结😄

黑体辐射与亮温度(Brightness Temperature)的定义

  我们知道，物体的热辐射谱是黑体谱，其谱仅用一个参数便可以去描述，那就是温度。黑体辐射的强度随频率$\nu$的变化可以用下式表示：

$B_\nu(\nu,T)=\frac{2h\nu^3}{c^2}\frac{1}{exp(\frac{h\nu}{kT})-1}~.$

  根据爱因斯坦的光电理论，对于电磁波而言，若把其看成粒子，那么其能量为$h\nu$。如果光子的频率越低，相对应波长$\lambda$越长，其能量就越低。那么对于射电频段，从下图可以看出，其对应的是波长较长的电磁波：

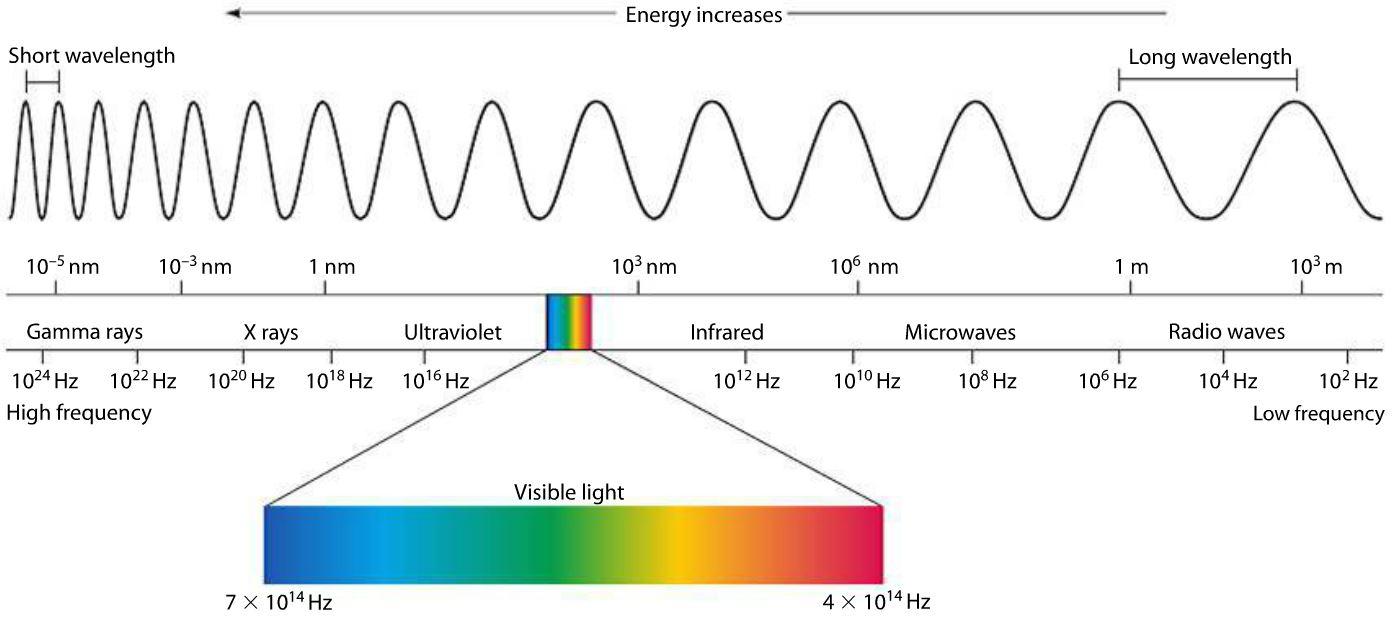
  所以，对于射电波而言($h\nu \ll kT$)，黑体辐射$B_\nu$便可以近似为如下形式：

$B_\nu \approx \frac{2kT\nu^2}{c^2}~,$

这个近似关系就是所谓的Rayleigh-Jeans law，至于为什么用这个名字，那是因为当年普朗克"造"出黑体辐射公式，其实是把两个关系拼接起来的，在长波段被称为Rayleigh-Jeans side，在短波段被称为Wien's side. 那么问题来了，我们为什么要折腾这么个近似式子出来呢？请仔细看上面的式子，左边$B_\nu$，如果不是黑体辐射，而是一般的情况，那么这个东西就是所谓的specific intensity $I_\nu$，如果我们此时固定频率$\nu$不变，那么这不就找到了在长波(射电)段的强度与温度的一一对应了嘛😄：

$T\approx \frac{B_\nu c^2}{2k\nu}~.$

  所以，重点来了，假设处在射电频段的发射某信号的源的辐射机制是黑体辐射，那么通过Rayleigh-Jeans law关系计算得到的温度，便称作亮温度, Brightness Temperature，$T_b$. ⚠️请注意，由于我们这里是假设源是黑体辐射，所以只有当其真正是黑体辐射的时候，这个温度$T_b$才代表真正的物理温度，否则这个温度仅仅是一个与$I_\nu$的等价量罢了，只不过是换了个单位。

那么，为啥要用温度来描述信号呢？

  在上面笔者介绍了黑体辐射以及亮温度的定义，现在可以开始回答开篇的问题了：为啥不直接用$I_\nu$来描述信号，而非要整个温度呢？难道是射电工作者比较有个性，要搞特殊特立独行😎？哈哈哈答案自然不是，其原因主要是因为在射电望远镜频段用于校准的时候，为了方便，通常人们会使用温度这个概念，且听我缓缓道来😁
  我们在天文领域使用的射电望远镜，如下图所示(图片来自Nakashima黑板手绘图)实际上工作的时候的流程是：接收到电磁波信号->将电磁波信号转换为电信号->控制台记录📝.

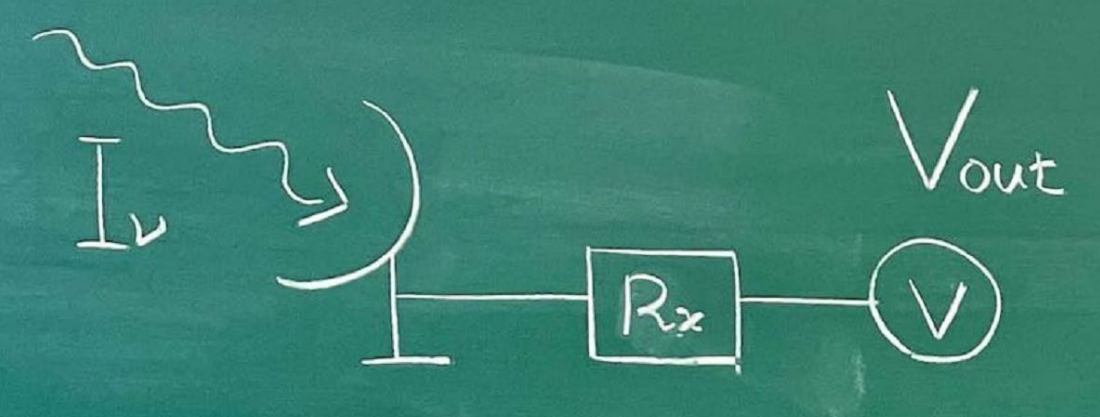
那么问题就来了，射电望远镜是一个复杂而庞大的系统，我们应该如何准确的找到观测信号与射电望远镜接收机最后输出的电信号之间的一一对应关系呢？读者不妨想一想我们的温度计🌡️是怎么制成的：举个例子，根据热力学第零定律，我们知道如何去定标一个水银温度计，比如我们记录水银在开水中的高度(假设就是严格的100°C)，然后我们再把温度计放到冰水混合物中(假设就是严格的0°C)，记录下此时的水银高度，现在我们就有了一个温度-水银高度的对应关系啦，在这个区间内做内插，既可以得到任意温度时候水银高度了，这个过程被称为校准，calibration
  那么🌡️温度计和我们的射电望远镜有啥关系呢？其实是一个道理，射电望远镜也需要进行校准。正如前面所说，射电望远镜系统很复杂，钢筋结构、自身电磁干扰等等可能都会影响到其获取的电信号，这一系列“噪音”，我们很难找到解析形式，所以最简单的办法，就是类似刚刚温度计那样去校准就vans了😁管他那么多，反正我只需要知道，比如，在下图中(图片来自Nakashima黑板手绘图)，当我放置一个300K的物体的时候，望远镜反馈的电压是多少；然后在记录一下放置77K的时候的电压是多少。有了这组对应关系，那么我们就可以进行内插或者外插，得到任意电压时候所对应的温度了，这就是射电望远镜的校准过程的一个粗略描述啦。在实际操作中，这个300K的玩意，一般被为hot load🔥，而较低温度的77K的玩意，被称为cold load🧊.

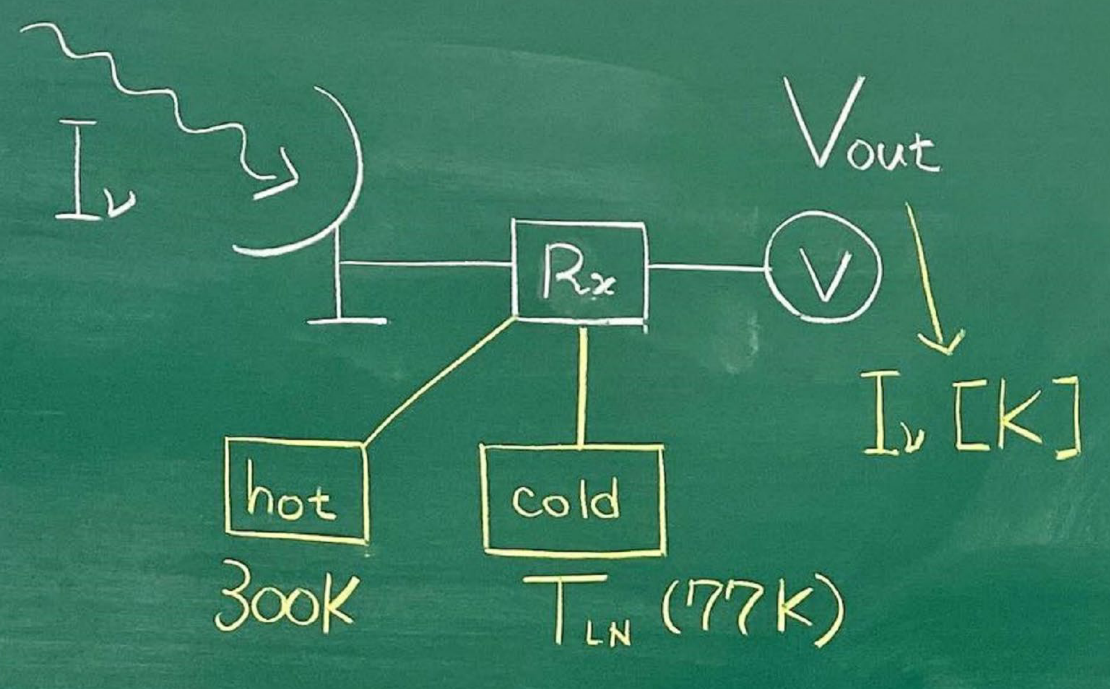
  那么相信看到这里，你已经知晓了为什么在射电天文领域，大家要用这么一个“模棱两可”的温度的概念来描述信号了吧。逻辑如下：

射电望远镜是把强度信号转换为电信号的机器
↓
射电望远镜需要校准
↓
使用符合黑体谱的🔥热+🧊冷的特定温度的源来校准
↓
得到亮温度T与电信号V之间的关系
↓
实际观测得到了电信号
↓
根据校准将电信号转换为亮温度

  以上，便是整套逻辑了，希望能够解答你的困惑😄